【他のレンジ/シート/ブックを更新する】
1 あるレンジから別レンジを更新
2 あるシートから別シートを更新
3 逆Z式並びで更新
4 セルで指定したシートを更新
5 複数シートを連続更新
6 関数の定義と呼び出し
7 Pythonの汎用型プログラム構成
逆Z式並びで更新
今回は、Python-xlwingsによって、5列×2行の逆Z式並びとなるように
行番号と列番号を算出しながらセルの値を更新します。
特定の列数毎に改行し表並びで表示
Pythonプログラム『PXS8024.py』では、『漢字入力帳』シートに用意した10問の漢字文字列を読みこみ、
『漢字学習帳』シートに漢字問題を、10列の横並びで書きこむという処理を実行しました。
次は、Python-xlwingsによって、『漢字入力帳』シートに用意した10問の漢字文字列を読みこみ、
『漢字学習帳』シートに漢字問題を、5列×2行の表並びで書きこむという処理を実行します。
問題番号の動きを図に表すと、次の図の水色の矢印のような動きになります。
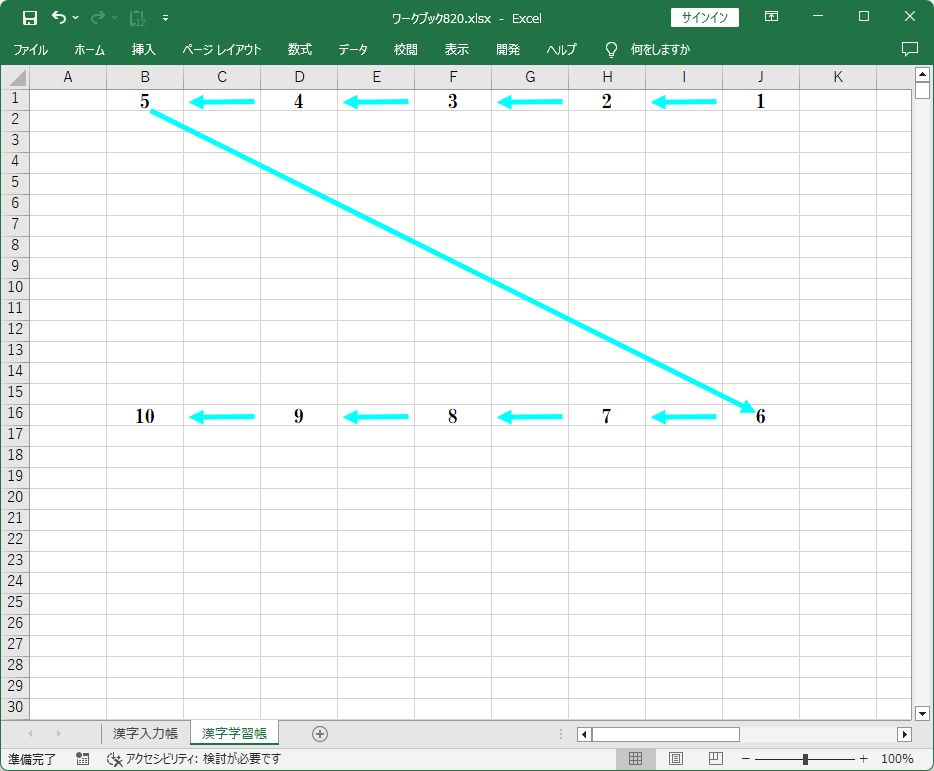
セル(1行,10列) → セル(1行,8列) → セル(1行,6列) → セル(1行,4列) → セル(1行,2列)
→ セル(2行,10列) → セル(2行,8列) → セル(2行,6列) → セル(2行,4列) → セル(2行,2列)という
順番で、それぞれのセルに問題番号 1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9 → 10 を書きこみます。
『Z』を左右逆にしたような並び方なので、今後、この並び方を『逆Z式並び』と呼ぶことにします。
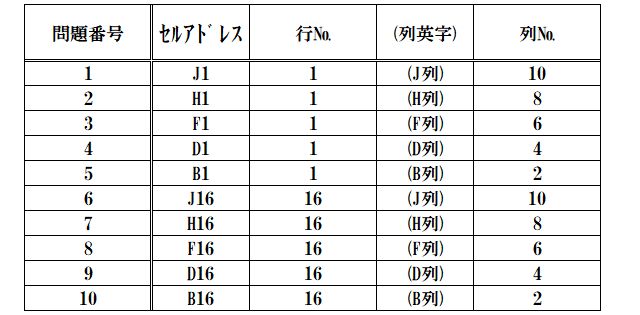
『逆Z式並び』で問題番号が書きこまれるセルアドレス・行・列の動きを表に表すと、
次の表のような動きになります。
先ず、Pythonプログラムファイルを保存しているフォルダ内に、
前回使用したExcelブック『ワークブック820.xlsx』をコピーして『ワークブック830.xlsx』を作成します。
次に、Pythonプログラム『PXS8024.py』をコピーして、Pythonプログラム『PXS8030.py』とします。
Pythonプログラム『PXS8024.py』では、『漢字入力帳』シートの最小行:『読取最小行』(2行目)から
最大行:『読取最大行』(11行目)のループの中で、漢字問題作成処理の最初に、
先頭行に問題番号を読み書きするプログラムコードを追加しました。
今回は、Python-xlwingsによって、その問題番号を元に、5列×2行の逆Z式並びとなるように
書込問題番号行と列番号を算出しながら『漢字学習帳』シートに問題番号及び漢字問題を
書きこむプログラムコードを追加してみます。
オブジェクト生成部・定数部を改修します。
Excelファイル『ワークブック830.xlsx』をメモリ上に読みこみWorkbookオブジェクト『wb』を生成
『wb』のExcelシート『漢字入力帳』を読みこみsheetオブジェクト『Est』を生成
『wb』のExcelシート『漢字学習帳』を読みこみsheetオブジェクト『Wst』を生成
定数『最大列』に『10』列目を代入
定数『書込列数』に『5』列目を代入
定数『書込ステップ列』に『-2』を代入
定数『書込問題番号最小行』に『1』行目を代入
定数『書込ステップ行』に『15』行目を代入
import xlwings as xw
wb = xw.Book(’ワークブック830.xlsx’)
Est = wb.sheets[’漢字入力帳’]
Wst = wb.sheets[’漢字学習帳’]
最大列 = 10
書込列数 = 5
Const 書込ステップ列 = -2
書込問題番号最小行 = 1
書込ステップ行 = 15
処理部を改修します。
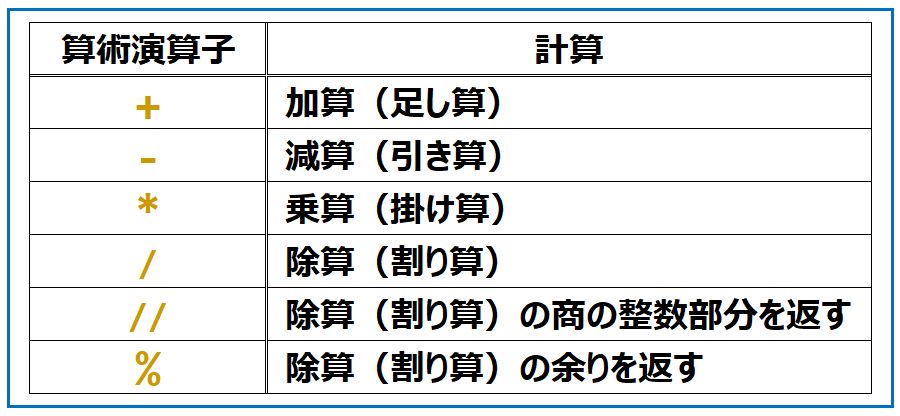
ここで、四則演算(加減乗除)などの算術計算を行うための記号『算術演算子』を紹介します。
Pythonで用意されている主な『算術演算子』を表にまとめると次のようになります。
足し算の『+』と引き算の『-』は、数学でつかう記号と同じでわかりやすいですが、
掛け算の『*』と割り算の『/』は、数学でつかう記号と違うので要注意です。
掛け算の『*』と割り算の『/』は、パソコンのキーボードに必ず割り当てられていて、
パソコン上の算術演算子の定番となっています。
『%』は割り算の余りを返すという特殊な算術演算子ですが、割り算の余りによって
列が確定するようなときに便利な算術演算子です。詳しくは後ほど紹介します。
『漢字入力帳』シートの最小行:『読取最小行』(2行目)から最大行:『読取最大行』(11行目)のループの中で、
漢字問題番号を取得し、その問題番号を元に5列×2行の表並びとなるように書込問題番号行と列番号を
算出しながら『漢字学習帳』シートに問題番号および漢字問題を書きこむプログラムコードを追加します。
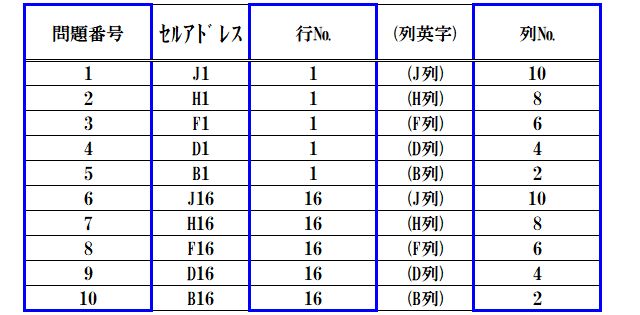
問題番号が書きこまれる行と列の動きを表に表すと、次の表のような動きになります。
特に青の罫線で囲んだ問題番号と行及び列の動きに着目してください。
以下、『漢字入力帳』シートの最小行:『読取最小行』(2行目)から最大行:『読取最大行』(11行目)の
ループの中にいるとイメージしてください。
(1) 書込問題番号行の算出
問題を元に書込問題番号行を算出します。
問題と書込問題番号行の関係は次の表のようになります。

この表によると、問題番号が1から5までは行が1、問題番号が6から10までは行が16となっています。
つまり、問題番号が5(=書込列数)の倍数になる毎に、
行が15(=書込ステップ行)ずつ増加しているということです。
試しに、問題番号を5(=書込列数)で割ってみます。
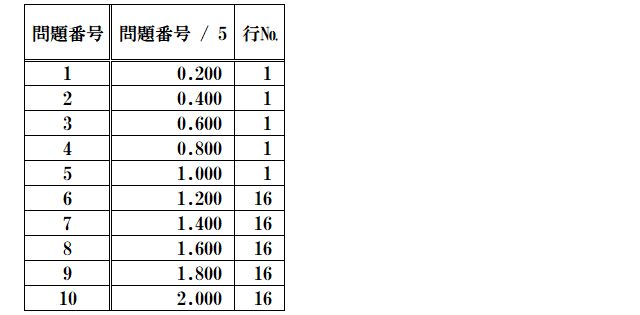
この問題番号 ÷ 5(=書込列数)の整数部分を取り出します。
Pythonでは引数の整数部分を取得する関数として、int関数が用意されています。
◇int関数:引数の整数部分を取得

このint関数をつかって問題番号÷5の整数部分を取り出したときの数値を表にします。
問題番号とint(問題番号 / 5)を比較してみると、
問題番号1~4は同じ数値0、問題番号5~9は同じ数値1、となっています。
問題番号1~5は同じ数値として0、問題番号6~10は同じ数値として1、となれば、
改行が上手くいきます。
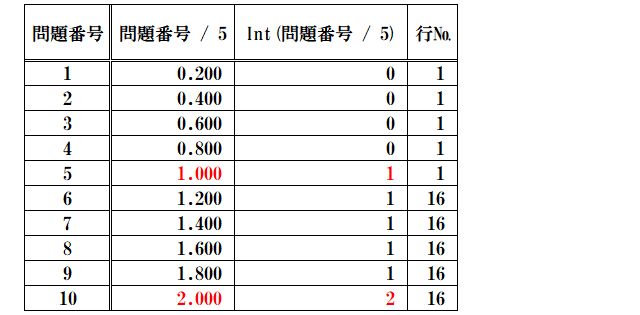
そこで、問題番号から1を引くことで、改行が上手くいくように調整します。
問題番号 – 1 を5(=書込列数)で割ってint関数をつかったときの数値を表にします。
問題番号1~5は同じ数値として0、問題番号6~10は同じ数値として1、となりました。
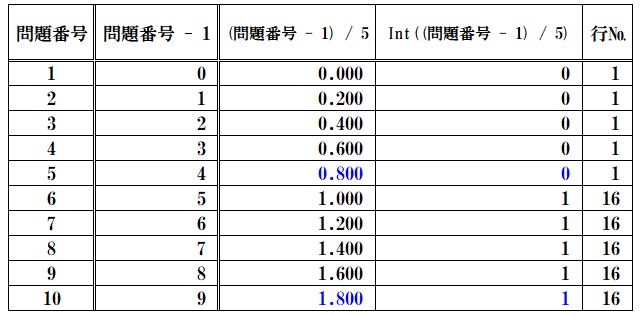
次は、問題番号1~5は同じ行として1、問題番号6~10は同じ行として16、
となるように調整していきます。
int((問題番号 - 1) / 5)に対して15(=書込ステップ行)を掛けたときの数値を表にします。
問題番号1~5は同じ数値として0、問題番号6~10は同じ数値として15、となりました。
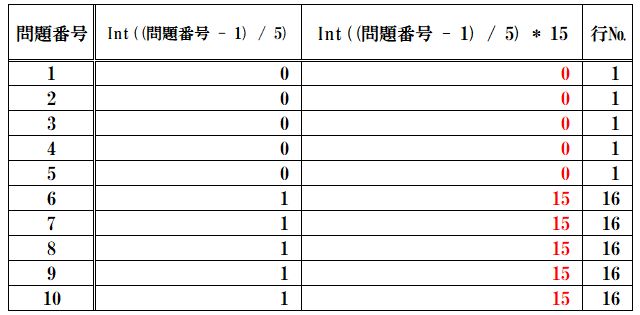
このint((問題番号 - 1) / 5)×15の数値と行を比較してみると、
行が、int((問題番号 - 1) / 5)×15より、1多くなっています。
そこで、int((問題番号 - 1) / 5) * 15に 1(=書込問題番号最小行)を加えることで、
行が正確な数値となるように調整します。
int((問題番号 - 1) / 5) * 15に 1(=書込問題番号最小行)を加えたときの数値を表にします。
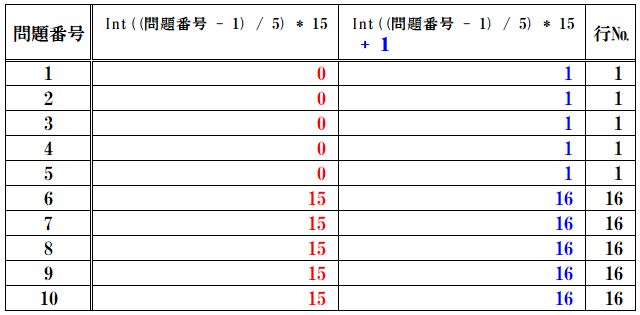
問題番号1~5は同じ行として1、問題番号6~10は同じ行として16、となり、
int((問題番号 - 1) / 5)×15 + 1 と 行 が、全て一致しました。
書込問題番号行の算出をプログラムコードにすると、
書込問題番号行 = int((問題番号 - 1) / 書込列数) * 書込ステップ行 + 書込問題番号最小行
となります。
更に、最小行の算出をプログラムコードにすると、
最小行 = 書込問題番号行 + 1
となります。
(2) 列番号の算出
問題を元に列番号を算出します。問題と列番号の関係は次の表のようになります。

この表によると、
問題番号が1のときは、列が10、
問題番号が2のときは、列が8、
問題番号が3のときは、列が6、
問題番号が4のときは、列が4、
問題番号が5のときは、列が2、
問題番号が6のときは、列が10、
問題番号が7のときは、列が8、
問題番号が8のときは、列が6、
問題番号が9のときは、列が4、
問題番号が10のときは、列が2、となっています。
つまり、問題番号を5(=書込列数)で割ったときの余りと列に関連性があるということです。
試しに、問題番号を5(=書込列数)で割ったときの余りを計算してみます。
Python-xlwingsには、割り算の余りを返すという算術演算子として、%算術演算子が用意されています。
◇%算術演算子:割り算の余りを返す

この%算術演算子をつかって問題番号 ÷ 5(=書込列数)の余りを計算したときの数値を表にします。
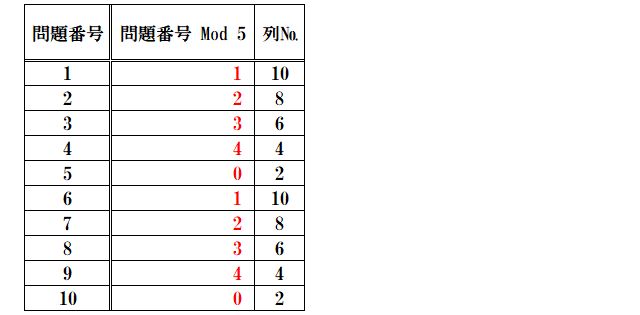
問題番号と問題番号 % 5を比較してみると、
問題番号が1のときは、数値1、
問題番号が2のときは、数値2、
問題番号が3のときは、数値3、
問題番号が4のときは、数値4、
問題番号が5のときは、数値0、
問題番号が6のときは、数値1、
問題番号が7のときは、数値2、
問題番号が8のときは、数値3、
問題番号が9のときは、数値4、
問題番号が10のときは、数値0、となっています。
一方、
問題番号が1のときは、列が10、
問題番号が2のときは、列が8、
問題番号が3のときは、列が6、
問題番号が4のときは、列が4、
問題番号が5のときは、列が2、
問題番号が6のときは、列が10、
問題番号が7のときは、列が8、
問題番号が8のときは、列が6、
問題番号が9のときは、列が4、
問題番号が10のときは、列が2、となっています。
開始列は10(=最大列)であるため、列が10(=最大列)のときは数値が0となるようにしておきたいところです。
そこで、問題番号から1を引くことで、列が10(=最大列)のときは数値が0となるように調整します。
%算術演算子をつかって、問題番号 – 1 を5(=書込列数)で割ったときの余りを表にします。
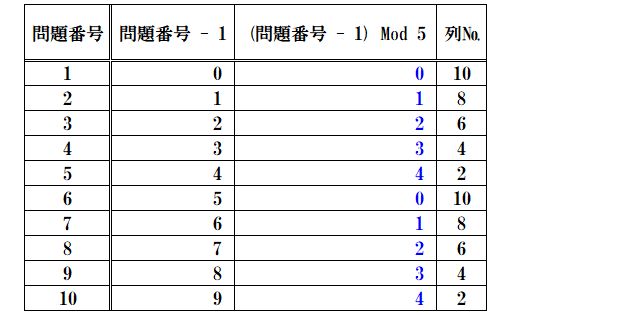
問題番号が1のときは、数値0、
問題番号が2のときは、数値1、
問題番号が3のときは、数値2、
問題番号が4のときは、数値3、
問題番号が5のときは、数値4、
問題番号が6のときは、数値0、
問題番号が7のときは、数値1、
問題番号が8のときは、数値2、
問題番号が9のときは、数値3、
問題番号が10のときは、数値4、となり、
列が10のときは数値が0となりました。
次は、
問題番号が1のときは、列が10、
問題番号が2のときは、列が8、
問題番号が3のときは、列が6、
問題番号が4のときは、列が4、
問題番号が5のときは、列が2、
問題番号が6のときは、列が10、
問題番号が7のときは、列が8、
問題番号が8のときは、列が6、
問題番号が9のときは、列が4、
問題番号が10のときは、列が2、となるように調整していきます。
10(=最大列)から、(問題番号 - 1) % 5に対して-2(=書込ステップ列)を掛けたものを引いた数値
を表にします。
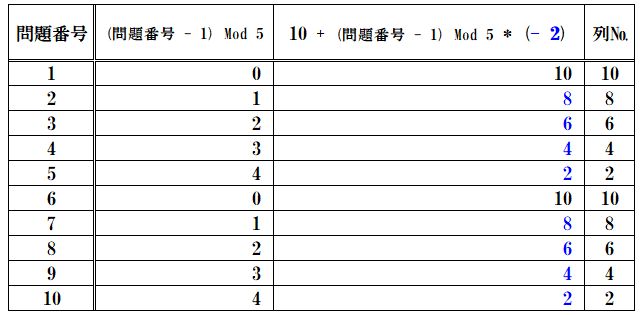
問題番号が1のときは、数値10となり、列が10、
問題番号が2のときは、数値8となり、列が8、
問題番号が3のときは、数値6となり、列が6、
問題番号が4のときは、数値4となり、列が4、
問題番号が5のときは、数値2となり、列が2、
問題番号が6のときは、数値10となり、列が10、
問題番号が7のときは、数値8となり、列が8、
問題番号が8のときは、数値6となり、列が6、
問題番号が9のときは、数値4となり、列が4、
問題番号が10のときは、数値2となり、列が2、となり、
10 + (問題番号 - 1) % 5 * (- 2) と 列 が、全て一致しました。
列番号の算出をプログラムコードにすると、
列番号 = 最大列 + ((問題番号 - 1) % 書込列数) * 書込ステップ列
となります。
(3) 以降のプログラムコード
以降、次のソースコードパネルのように、
変数『書込問題番号行』、変数『列番号』、変数『行番号』、変数『枠領域』を更新しながら、
その値によりセル位置を指定し、
問題の更新、1文字書き込み、枠の設定、ふりがなの更新を実行します。
【ソースコードパネル】
# PXS8030.py
import xlwings as xw
wb = xw.Book(’ワークブック830.xlsx’)
Est = wb.sheets[’漢字入力帳’]
読取問題番号列 = 1
読取列 = 2
最大枠数 = 4
漢字最小列 = 3
漢字最大列 = 6
読取最小行 = 2
Wst = wb.sheets[’漢字学習帳’]
# 最小列 = 20
最大列 = 10
書込列数 = 5
書込ステップ列 = -2
書込問題番号最小行 = 1
# 書込問題番号行 = 1
書込ステップ行 = 15
# 最小行 = 2
読取最大行 = Est.range(Est.cells.last_cell.row, 2).end('up').row
# 列番号 = 最小列
# ===== 読取行の最小行から最大行へのループにより読取行をカウントアップ =====
for 読取行 in range(読取最小行, 読取最大行 + 1):
問題番号 = Est.range(読取行, 読取問題番号列).value
書込問題番号行 = int((問題番号 - 1) / 書込列数) * 書込ステップ行 \
+ 書込問題番号最小行
最小行 = 書込問題番号行 + 1
列番号 = 最大列 + ((問題番号 - 1) % 書込列数) * 書込ステップ列
列英字名 = Wst.range(1, 列番号).get_address \
(False, False).replace("1", "")
枠領域 = 列英字名 + str(書込問題番号行)
Wst.range(枠領域).value = 問題番号
Wst.range(枠領域).api.Font.Size = 10
txt = Est.range(読取行, 読取列).value
最大文字数 = len(txt)
# ===== 文字列の先頭文字から最終文字へのループにより位置インデックスをカウントアップ =====
for 位置インデックス in range(0, 最大文字数):
行番号 = 最小行 + 位置インデックス
Wst.range(行番号, 列番号).value = txt[位置インデックス]
# ===== 漢字列の最小列から最大列へのループにより漢字列をカウントアップ =====
for 漢字列 in range(漢字最小列, 漢字最大列 + 1):
漢字名 = Est.range(読取行, 漢字列).value
if 漢字名 is not None:
位置インデックス = Est.range(読取行, 読取列).value.find(漢字名)
if 位置インデックス >= 0:
行番号 = 最小行 + 位置インデックス
列英字名 = Wst.range(1, ふりがな列).get_address \
(False, False).replace("1", "")
枠領域 = 列英字名 + str(行番号)
Wst.range(枠領域).api.Borders.LineStyle = 1
Wst.range(枠領域).value = ""
ふりがな読取列 = 漢字列 + 最大枠数
ふりがな名 = Est.range(読取行, ふりがな読取列).value
if ふりがな名 is not None:
ふりがな列 = 列番号 + 1
列英字名 = Wst.range(1, ふりがな列).get_address \
(False, False).replace("1", "")
枠領域 = 列英字名 + str(行番号)
Wst.range(枠領域).value = ふりがな名
Wst.range(枠領域).api.Font.Size = 8
Wst.range(枠領域).api.HorizontalAlignment = -4131
Wst.range(枠領域).api.Orientation = -4166
Wst.range(枠領域).api.ShrinkToFit = True
# 列番号 = 列番号 + 書込ステップ列
それでは、このPythonプログラムを実行してみます。
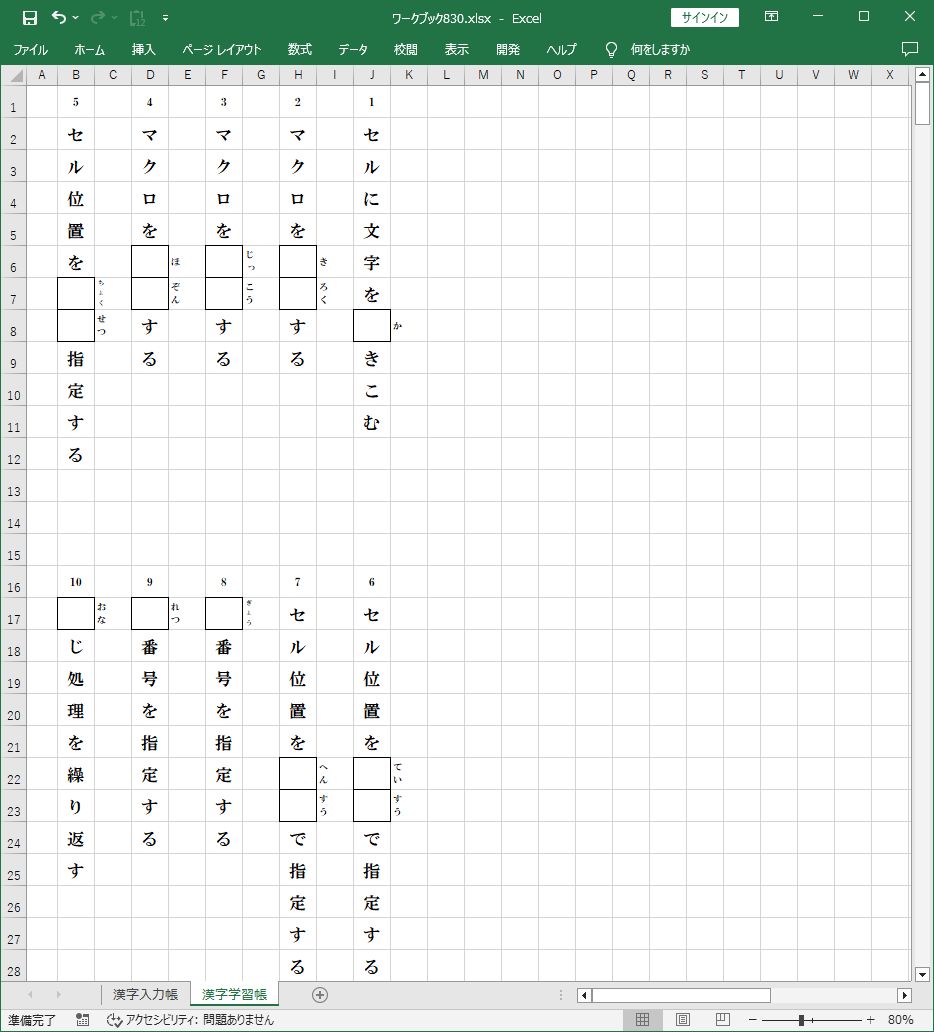
『漢字入力帳』シートに用意した10問の漢字文字列が、文字分割されて『漢字学習帳』シートに、
『逆Z式並び』で書きこまれました。










